Vecto pháp tuyến là gì?
Vectơ pháp tuyến (tiếng Anh: normal vector) là một khái niệm trong toán học và đại số tuyến tính. Nó được định nghĩa là một vectơ vuông góc với một mặt phẳng hay một đường cong tại một điểm nào đó.
Cụ thể, với một mặt phẳng trong không gian ba chiều, vectơ pháp tuyến là một vectơ không giống với bất kỳ vectơ nào nằm trong mặt phẳng đó và vuông góc với tất cả các vectơ nằm trên mặt phẳng đó. Nói cách khác, nếu bạn đặt một tấm bìa lên mặt phẳng đó và nhấn chặt bằng tay, thì vectơ pháp tuyến sẽ trỏ lên phía trên của tấm bìa đó.
Trong các ứng dụng thực tế, vectơ pháp tuyến thường được sử dụng để tính toán phép chiếu của một điểm hoặc một đối tượng lên một mặt phẳng hay một đường cong. Nó cũng được sử dụng trong định lý Stokes và các bài toán về tích phân đường cong.
Tính chất vecto pháp tuyến
Một số tính chất cơ bản của vectơ pháp tuyến bao gồm:
– Vectơ pháp tuyến là một vectơ vuông góc với mặt phẳng hay đường cong tại điểm đó.
– Độ dài của vectơ pháp tuyến là độ dài nhỏ nhất có thể của các vectơ nằm trên mặt phẳng hay đường cong tại điểm đó.
– Nếu có hai mặt phẳng song song với nhau, thì các vectơ pháp tuyến của hai mặt phẳng này là bằng nhau.
– Đối với một mặt phẳng trong không gian ba chiều, nếu ta biết hai vectơ nằm trên mặt phẳng đó và đi qua một điểm trên mặt phẳng đó, thì ta có thể tính được vectơ pháp tuyến của mặt phẳng đó bằng cách tính tích vô hướng của hai vectơ này và lấy đạo hàm theo một biến số.
– Vectơ pháp tuyến của một đường cong tại một điểm chính là vectơ pháp tuyến của mặt tiếp tuyến của đường cong tại điểm đó.
– Trong đại số tuyến tính, vectơ pháp tuyến của một không gian con của không gian nào đó được định nghĩa là vectơ pháp tuyến của mặt phẳng hay đường cong mà không gian con đó tạo thành.
Cách tìm vecto pháp tuyến của đường thẳng
Để tìm vectơ pháp tuyến của một đường thẳng trong không gian ba chiều, ta có thể làm như sau:
– Xác định hai vector định hướng của đường thẳng: Ví dụ, nếu đường thẳng được biểu diễn dưới dạng phương trình tham số là:
x = x0 + at y = y0 + bt z = z0 + ct
thì hai vector định hướng của đường thẳng sẽ là:
v = <a, b, c>
w = <1, 0, 0> (hoặc <0, 1, 0>, <0, 0, 1> tùy chọn)
– Tính tích vô hướng của hai vector định hướng của đường thẳng:
v x w = <b, -a, 0>
– Tính đơn vị của vectơ pháp tuyến:
n = (v x w) / ||v x w||
trong đó ||v x w|| là độ dài của vectơ v x w.
Lưu ý rằng cách tính này chỉ áp dụng được cho đường thẳng không song song với mặt phẳng xy (hoặc đường thẳng song song với mặt phẳng xy nhưng không song song với hai trục x và y). Nếu đường thẳng song song với mặt phẳng xy hoặc nằm trên hai trục x hoặc y, vectơ pháp tuyến của đường thẳng sẽ không xác định được bằng cách này.
Phương trình tham số của đường thẳng
Phương trình tham số của đường thẳng trong không gian ba chiều là một cách biểu diễn đường thẳng dưới dạng của hai phương trình tham số tuyến tính. Một đường thẳng có thể được xác định bởi hai điểm trên đường thẳng hoặc bởi một điểm trên đường thẳng và một vector định hướng của đường thẳng đó.
Giả sử đường thẳng có vector định hướng là v = <a, b, c> và điểm trên đường thẳng là P = (x0, y0, z0). Để xác định phương trình tham số của đường thẳng, ta lấy một điểm Q = (x, y, z) trên đường thẳng và viết phương trình vector của đoạn thẳng PQ như sau:
PQ = <x – x0, y – y0, z – z0>
Vì PQ song song với v nên tồn tại một số thực t tương ứng với Q sao cho:
PQ = t*v
Khi đó, phương trình tham số của đường thẳng có thể được viết dưới dạng:
x = x0 + at
y = y0 + bt
z = z0 + ct
Trong đó, a, b, c là các tham số thực và (x, y, z) là tọa độ của một điểm bất kỳ trên đường thẳng.
Lưu ý rằng phương trình tham số này không phải là duy nhất và có thể có nhiều cách biểu diễn khác nhau cho cùng một đường thẳng.
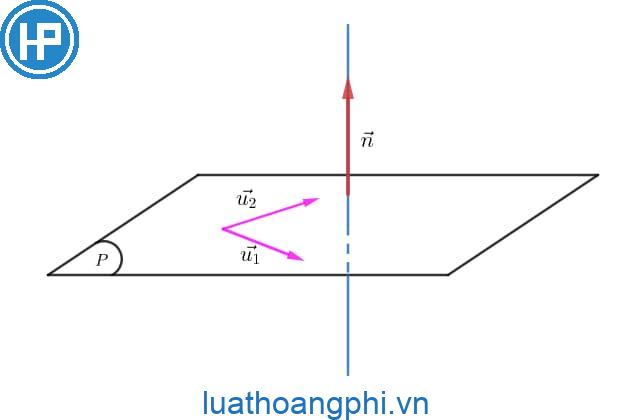
Vecto chỉ phương là gì?
Vectơ chỉ phương là một vectơ không có định hướng hay hình dạng, chỉ có giá trị và hướng của nó. Nó thường được sử dụng để biểu diễn hướng của một đối tượng trong không gian ba chiều hoặc trong không gian n chiều.
Một vectơ chỉ phương được định nghĩa bởi độ lớn (magnitude) của nó và hướng (direction) của nó. Độ lớn của vectơ chỉ phương thường được định nghĩa bằng cách lấy căn bậc hai của tổng bình phương các thành phần của vectơ, trong khi hướng của nó được định nghĩa bởi một đường thẳng trong không gian.
Vectơ chỉ phương có thể được sử dụng để biểu diễn hướng của ánh sáng, của lực, của tốc độ hay của bất kỳ đối tượng nào khác trong không gian. Chúng có ứng dụng rất rộng trong đa dạng lĩnh vực như đồ họa máy tính, vật lý, toán học, kỹ thuật, v.v.
1 đường thẳng có bao nhiêu vectơ pháp tuyến
Một đường thẳng trong không gian ba chiều có vô số vectơ pháp tuyến.
Một vectơ pháp tuyến của đường thẳng là một vectơ vuông góc với đường thẳng đó và có hướng không đổi trên đường thẳng. Vì một đường thẳng có thể có nhiều hướng khác nhau, do đó có vô số vectơ pháp tuyến của một đường thẳng.
Tuy nhiên, trong trường hợp của không gian hai chiều, đường thẳng chỉ có một vectơ pháp tuyến duy nhất.
Một số bài tập tìm vecto pháp tuyến của đường thẳng
Dưới đây là một số bài tập tìm vectơ pháp tuyến của đường thẳng:
Bài tập 1: Tìm vectơ pháp tuyến của đường thẳng qua hai điểm A(1,2,3) và B(4,5,6).
+ Để tìm hai vector trên đường thẳng, ta có thể tính vector kết nối giữa A và B: AB = (4-1)i + (5-2)j + (6-3)k = 3i + 3j + 3k = 3(i+j+k)
+ Tích có hướng của hai vector đó: AB × (i+j+k) = begin{vmatrix} i & j & k 3 & 3 & 3 1 & 1 & 1 end{vmatrix} = 0i – 6j + 6k
+ Lấy vectơ đơn vị của tích có hướng để được vectơ pháp tuyến: n = (-1/sqrt(2))j + (1/sqrt(2))k
Vậy vectơ pháp tuyến của đường thẳng đó là n = (-1/sqrt(2))j + (1/sqrt(2))k.
Bài tập 2: Tìm vectơ pháp tuyến của đường thẳng có phương trình tham số: x = 1 + 2t y = 3 – t z = 4 + 4t
+ Hai vector trên đường thẳng có thể được tính bằng cách lấy hai điểm bất kỳ
+ Lấy hai điểm trên đường thẳng, chẳng hạn A(1,3,4) với t = 0 và B(3,2,8) với t = 1.
+ Tính vector kết nối giữa hai điểm đó: AB = (3-1)i + (2-3)j + (8-4)k = 2i – j + 4k
+ Vector pháp tuyến được tính bằng tích có hướng của hai vector: AB × (i+j+k) = begin{vmatrix} i & j & k 2 & -1 & 4 1 & 1 & 1 end{vmatrix} = -5i – 6j + 3k
+ Lấy vectơ đơn vị của tích có hướng: n = (-5/sqrt(70))i – (6/sqrt(70))j + (3/sqrt(70))k
Vậy vectơ pháp tuyến của đường thẳng đó là n = (-5/sqrt(70))i – (6/sqrt(70))j + (3/sqrt(70))k.
Bài tập 3: Tìm vectơ pháp tuyến của đường thẳng có phương trình tham số: x = 3t y = 2t z = 1 + 5t
+ Hai vector trên đường thẳng có thể được tính bằng cách lấy hai điểm bất kỳ trên đường thẳng.
+ Chọn hai điểm là A(0,0,1) với t = 0 và B(3,2,16) với t = 3.
+ Tính vector kết nối giữa hai điểm đó: AB = (3-0)i + (2-0)j + (16-1)k = 3i + 2j + 15k
+ Tính tích có hướng của hai vector: AB × (i+j+k) = begin{vmatrix} i & j & k 3 & 2 & 15 1 & 1 & 1 end{vmatrix} = 13i – 12j + 1k
+ Lấy vectơ đơn vị của tích có hướng: n = (13/sqrt(170))i – (12/sqrt(170))j + (1/sqrt(170))k
Vậy vectơ pháp tuyến của đường thẳng đó là n = (13/sqrt(170))i – (12/sqrt(170))j + (1/sqrt(170))k.
Trên đây là một số thông tin liên quan đến Vecto pháp tuyến là gì? Cách tìm vecto pháp tuyến của đường thẳng? tại chuyên mục Toán học?, Quý độc giả có thể tham khảo các bài viết khác liên quan tại website: luathoangphi.vn
