Trong nội dung bài viết này, chúng tôi sẽ chia sẻ tới Quý độc giả các thông tin hữu ích về Vị trí tương đối của hai đường thẳng trong không gian. Mời Quý vị tham khảo:
Vị trí tương đối của hai đường thẳng trong không gian
Trong không gian, với hai đường thẳng, có thể xảy ra các trường hợp sau đây:
Thứ nhất: Hai đường thẳng đồng phẳng
Hai đường thẳng đồng phẳng hay ở trên cùng một mặt phẳng có thể xảy ra 3 vị trí tương đối là:
1/ Cắt nhau: Có duy nhất 1 điểm chung
2/ Song song: không có điểm chung
3/ Trùng nhau: Có nhiều hơn hai điểm chung
Thứ hai: Hai đường thẳng không đồng phẳng
Đây là trường hợp mà hai đường thẳng không có điểm chung, còn gọi là hai đường thẳng chéo nhau.
Như vậy, để xét vị trí tương đối của hai đường thẳng trong không gian, ta có thể xét theo hai tiêu chí, đó là số điểm chung và sự đồng phẳng.
Tuy nhiên, trong Oxyz thì xét theo hai tiêu chí như vậy sẽ không hiệu quả và gặp nhiều khó khăn, tính toán dài dòng. Để thực hiện xét nhanh vị trí tương đối của hai đường thẳng trong không gian Oxyz, ta sử dụng tính chất có hướng và xét theo sơ đồ.
Xét vị trí tương đối của hai đường thẳng trong không gian
Thứ nhất: Phương pháp giải
Vị trí tương đối giữa đường thẳng d (đi qua M0 và có vectơ chỉ phương u→) và đường thẳng d’ (đi qua M’0 và có vectơ chỉ phương u’→)
– d và d’ cùng nằm trong một mặt phẳng ⇔
– d ≡ d’⇔
– d // d’ ⇔
– d và d’ cắt nhau: ⇔
– d và d’ chéo nhau ⇔
–
Thứ hai: Ví dụ
Ví dụ 1:
Xác định vị trí tương đối của hai đường thẳng sau:
A. Cắt nhau
B. Trùng nhau
C. Chéo nhau
D. Song song
Hướng dẫn giải
Đường thẳng d có vecto chỉ phương và đi qua M0 (0;1;2)
Đường thẳng d’ có vecto chỉ phương
Nên hai đường thẳng d và d’ song song.
=> Chọn D.
Ví dụ 2:
Tìm a để hai đường thẳng sau đây song song:
A. a= 2
B. a= -3
C. a= -2
D. a= 4
Hướng dẫn giải
Đường thẳng d và d’ có vecto chỉ phương lần lượt là
Để d // d’ thì
Khi đó đường thẳng d’ đi qua điểm N (1; 2; 2) và điểm N không thuộc d.
Vậy d // d’ khi và chỉ khi a = 2
=> Chọn A.
Ví dụ 3:
Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng . Khi đó, giá trị của m bằng bao nhiêu thì d1 cắt d2?
A. m= 0
B. m= 1
C. m= -2
D. Đáp án khác
Hướng dẫn giải
+ Đường thẳng d1: đi qua A(1; 0; 1) và nhận vecto làm vecto chỉ phương
+ Đường thẳng d2: đi qua B(0; -2; -m) và nhận vecto làm vecto chỉ phương
+ để hai đường thẳng d1 và d2 cắt nhau thì:
⇔ – 3.( -1) – 1( – 2) + 5( – m- 1) =0 ⇔ 3+ 2- 5m- 5= 0 ⇔ 5m= 0 ⇔ m= 0
=> Chọn A.
Ví dụ 4:
Cho hai đường thẳng . Tìm m để hai đường thẳng đã cho chéo nhau?
A. m ≠ -1
B. m ≠ -10
C. m ≠ 10
D. m ≠ 12
Hướng dẫn giải
+ Đường thẳng d1 đi qua A( 2; 0;-1) và có vecto chỉ phương .
+ Đường thẳng d2 đi qua B( 0; m; – 1) và có vecto chỉ phương
+ Để hai đường thẳng đã cho chéo nhau khi và chỉ khi: ⇔ 10+ m ≠ 0 hay m ≠ -10
=> Chọn B.
Bài tập về xét vị trí tương đối của hai đường thẳng trong không gian
Bài tập 1:
Trong hệ tọa độ không gian Oxyz, cho đường thẳng . Chọn khẳng định đúng?
A. d1; d2 chéo nhau.
B. d1; d2cắt nhau.
C. d1; d2 vuông góc với nhau.
D. d1; d2 chéo nhau và vuông góc với nhau.
Hướng dẫn giải
+ Đường thẳng d1 đi qua A( 0; -1; 0); có vecto chỉ phương
+ Đường thẳng d2 đi qua B(0; 1; 1); có vecto chỉ phương
Ta có
=> Hai vecto vuông góc với nhau. suy ra đường thẳng d1 vuông góc với d2.
+ Mặt khác
Suy ra d1 và d2 chéo nhau.
=> Chọn D.
Bài tập 2:
Trong không gian Oxyz, cho hai đường thẳng 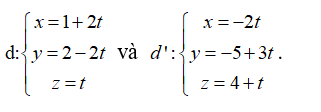
A. song song.
B. trùng nhau.
C. chéo nhau.
D. cắt nhau.
Hướng dẫn giải
Đường thẳng d có VTCP và đi qua M(1;2; 0)
Đường thẳng d’ có VTCP và đi qua M’(0;-5; 4)
Từ đó ta có:
Lại có
Suy ra d chéo nhau với d’.
=> Chọn C.
