chuc1803@gmail.com, bis.net.vn
1. 1.Sơ lược về AHP
Phương pháp phân tích thứ bậc AHP (Analytic Hierarchy Process – AHP) là một trong những phương pháp ra quyết định đa điều kiện (Multiple Criteria decision Making) được đề xuất bởi Thomas L. Saaty (1980), một nhà toán học người gốc Irắc. AHP là một phương pháp định lượng, dùng để đánh giá các phương án và chọn một phương án thỏa mãn các tiêu chí cho trước. Thay vì yêu cầu một khối lượng dữ liệu lớn, AHP sử dụng ý kiến chuyên gia và không cần quá nhiều dữ liệu để phân tích. Phương pháp AHP với 3 bước chính, đó là phân tích, đánh giá và tổng hợp. AHP trả lời các câu hỏi “Nên chọn phương án nào?” hay “Phương án nào tốt nhất?”.
Các bước thực hiện phân tích AHP
Bước #1. Xây dựng cấu trúc thứ bậc của bài toán: Xác định mục tiêu (Goal), các tiêu chí đánh giá (Criteria) và các phương án lựa chọn (Alternative)
Bước #2. Tính toán trọng số của từng tiêu chí (criteria)
o Xây dựng ma trận so sánh cặp cho mỗi tiêu chí
o Tính trọng số cho từng tiêu chí
o Kiểm tra tỷ số nhất quán CR (Consistency Ratio: CR<10%)
Bước #3. Tính mức độ ưu tiên cho từng phương án và chọn phương án tốt nhất
2. Minh họa về AHP
Trong ví dụ này minh họa phân tích AHP để đánh giá trọng số các tiêu chí lựa chọn mua điện thoại.
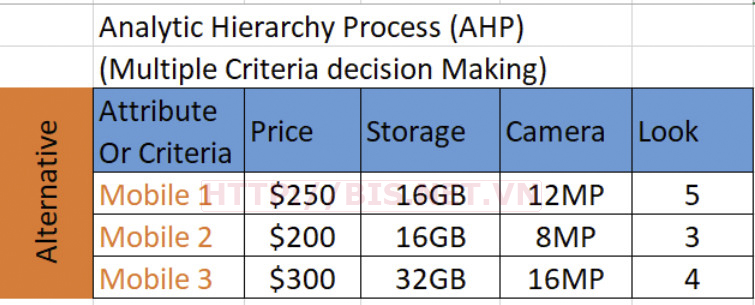
Xây dựng cấu trúc thứ bậc của bài toán:
Xác định mục tiêu (Goal): Mua điện thoại phù hợp nhất
Các tiêu chí đánh giá (Criteria): Có 4 tiêu chí là Giá (Price), Bộ nhớ (Storage), Camera, và Cảm nhận (Look)
Các phương án lựa chọn (Alternative): Có 3 phương án lựa chọn Mobile1, Mobile2, Mobile3
Xây dựng ma trận so sánh cặp cho mỗi tiêu chí (Pair- wise Comparison Matrix)
Dựa vào ý kiến của chuyên gia so sánh, đánh giá mức độ quan trọng giữa các tiêu chí theo từng cặptheo thang điểm đánh giá của T.Saaty:
Giả sử có kết quả ma trận so sánh cặp như sau: Chú ý ma trận này đường chéo có giá trị là 1 vì tiêu chí so sánh với chính nó (có mức độ quan trọng như nhau). Giá trị ở hàng 1 cột 2 là 5 có nghĩa là tiêu chí về giá có mức độ quan trọng gấp 5 lần tiêu chí về bộ nhớ, và như vậy thì giá trị ở hàng 2 cột 1 là 1/5 (bộ nhớ ít quan trọng hơn giá 5 lần).

Từ ma trận trên thêm hàng Sum để tính tổng theo cột như bên dưới:
Chuẩn hóa ma trận so sánh cặp bằng cách lấy giá trị của mỗi ô chia cho tổng theo cột
Normalised Pair-wise matrix (cell/sum by column)
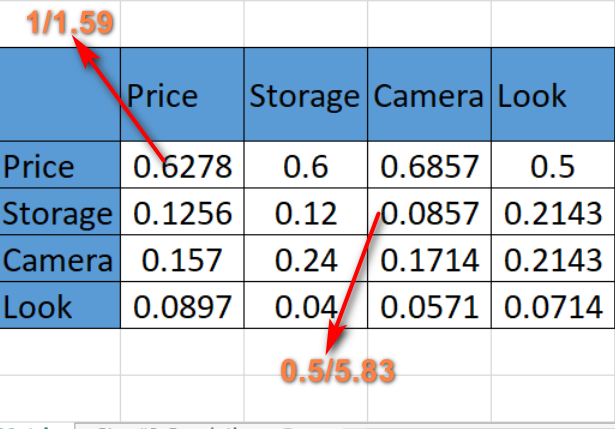
Tính trọng số cho các tiêu chí (trung bình theo hàng)

Sử dụng trọng số của các tiêu chí và ma trận so sánh cặp để tính tỷ số nhất quán CR (Consistency Rate) như sau:
Tính vector nhất quán (Consistency vector): Lấy tổng trọng số của các tiêu chí chia cho trọng số của từng tiêu chí
Tính giá trị riêng lớn nhất của ma trận so sánh (Lamdamax). Nếu Lamdamax càng gần bằng số tiêu chí so sánh thì tính phù hợp càng cao). Lamdamax được tính là trung bình cộng của vector nhất quán
Lamdamax=(4.1764+4.0222+4.1550+4.0494)/4=4.1007
Tính chỉ số nhất quán CI (Consistency Index)

Trong đó n là số tiêu chí so sánh cùng cấp
CI=(4.1007-4)/(4-1)= 0.03357
Tính tỷ số nhất quán CR (Consistency Ratio)
Trong đó: CI: Chỉ số nhất quán
RI (Random Index): Chỉ số ngẫu nhiên, được tra cứu theo số tiêu chí so sánh trong bảng sau: Bảng chỉ số ngẫu nhiên ứng với số tiêu chí lựa chọn được xem xét
Trong ví dụ này số tiêu chí là 4 nên RI =0.90
CR=0.03357/0.90 =0.037296 (<10%). Tỷ số nhất quán CR nhỏ hơn 10% thì phù hợp
Từ đó ta có thể sử dụng trọng số các tiêu chí để đánh giá phương án lựa chọn.
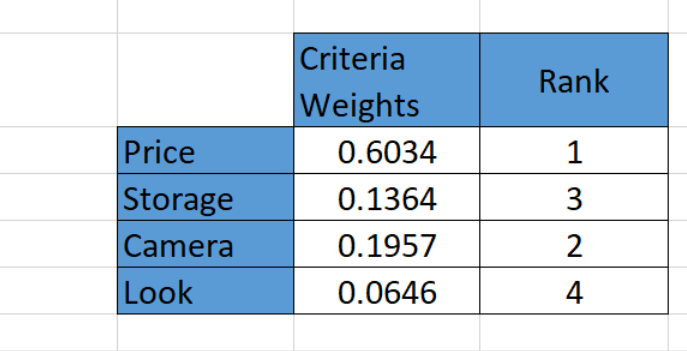
Bước 3: Tính độ ưu tiên của các phương án theo từng tiêu chí.
