Chắc hẳn các bạn học sinh đôi lúc sẽ gặp khó khăn với các câu hỏi Hai góc tương ứng là gì? Hai cạnh tương ứng là gì? Cách xác định góc tương ứng như thế nào?. Để trả lời cho các câu hỏi đó GiaiToan.com xin giới thiệu đến bạn đọc tài liệu Hai góc tương ứng bằng nhau gồm các kiến thức trọng tâm và trực quan giúp học sinh dễ hiểu, dễ nhớ, áp dụng vào làm bài tập tốt. Hy vọng đây sẽ là tài liệu hữu ích cho các em học sinh lớp 7 ôn tập và nâng cao kiến thức môn Toán 7.
A. Hai góc tương ứng là gì?
Hướng dẫn giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Ví dụ trực quan: 
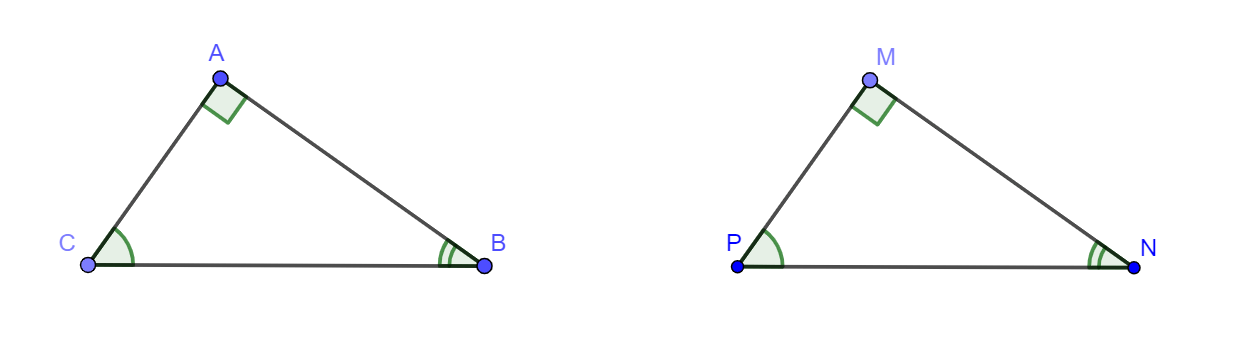
B. Hai cạnh tương ứng là gì?
Hai cạnh tương ứng là hai cạnh của hai tam giác khác nhau. Hai cạnh đó bằng nhau và nằm trong hai tam giác bằng nhau
Ví dụ trực quan: 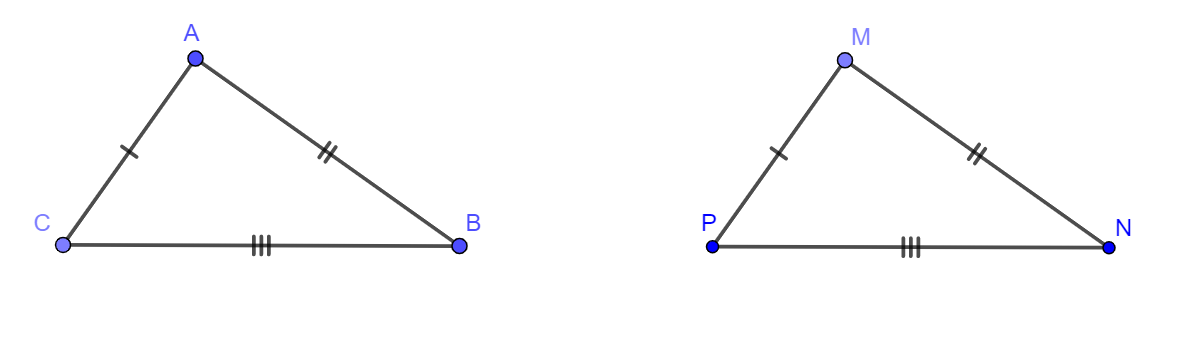
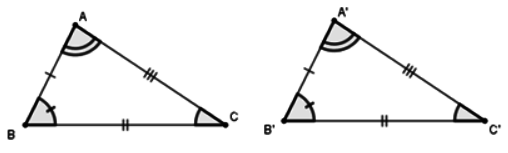
C. Hai tam giác nhau
Hai tam giác bằng nhau là hai tam giác có các canhj tương ứng bằng nhau và các góc tương ứng bằng nhau.
–
Hy vọng tài liệu trên sẽ giúp các em học sinh ghi nhớ lý thuyết về tam giác từ đó vận dụng giải các bài toán về tam giác một cách dễ dàng hơn. Chúc các em học tốt.
Ngoài ra GiaiToan mời thầy cô và học sinh tham khảo thêm một số tài liệu học tập liên quan:
- Tính chất ba đường trung trực của tam giác
- Tìm đa thức một biến có nghiệm cho trước
- Chứng minh đa thức không có nghiệm
- Chứng minh trong tam giác vuông cạnh huyền lớn hơn mỗi cạnh góc vuông
- Cho biết x và y là 2 đại lượng tỉ lệ thuận, khi x = 10 thì y = 5. Vậy khi x=-5 thì y=?
- Giá trị tuyệt đối của số hữu tỉ x được xác định như thế nào?
- Bài tập Toán 7 Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Cho tam giác ABC vuông tại A đường phân giác BE Kẻ EH vuông góc với BC (H thuộc BC), gọi K là giao điểm của AB và HE. Chứng minh rằng: a, Tam giác ABE = tam giác HBE b, BE là đường trung trực của đoạn thẳng AH c, EK = EC d, AE < EC e, BE vuông góc với KC
- Cho tam giác ABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc với BC (H thuộc BC). a, Chứng minh HB = HC b, Tính độ dài AH. c, Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE cân. d, So sánh HD và HC.
- Tìm tất cả các số tự nhiên thỏa mãn tổng của nó với các chữ số của nó bằng 2004
- Chứng minh rằng nếu p và q là các số nguyên tố lớn hơn 3 thì ta có (p – 1)(p + 1)(q – 1)(q + 1) luôn chia hết cho 576
-
Cho tam giác ABC cân tại A (góc A nhỏ hơn 900). Vẽ BH ⊥ AC (H thuộc AC), CK ⊥ AB (K thuộc AB).
a) Chứng minh rằng AH = AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A.
-
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh rằng:
a) HB = HC.
b) Góc BAH = Góc CAH
-
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE.
a) So sánh góc ABD và góc ACE
b) Gọi I là giao điểm
