Đường tròn lượng giác lớp 11 là phần kiến thức không thể không biết và không thể không hiểu. Học sinh có thể ứng dụng đường tròn lượng giác để giải nhanh câu hỏi trắc nghiệm Toán và Vật lí. Vì vậy các em cần nắm chắc các kiến thức cơ bản dưới đây.
Bí quyết chinh phục điểm cao lớp 11: Trọn bộ lí thuyết bài tập 8 môn chính khóa, nhanh chóng giành điểm 9 10 thi học kì

Các kiến thức cơ bản về đường tròn lượng giác bắt buộc phải nhớ
Những kiến thức cơ bản về đường tròn lượng giác lớp 11
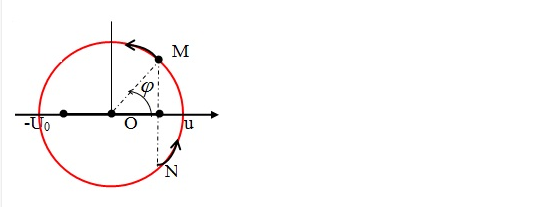
– Khái niệm: Đường tròn lượng giác là đường tròn đơn vị, định hướng ( quy ước chiều dương là chiều ngược kim đồng hồ) và trên đó chọn điệm A làm gốc.
– Điểm M(x;y) trên đường tròn lượng giác sao cho (OA; OM) = α được gọi là điểm trên đường tròn lượng giác biểu diễn cung (góc) lượng giác có số đo α.
Trục Ox được gọi là trục giá trị của cos.
Trục Oy được gọi là trục giá trị của sin.
Trục At gốc A cùng hướng với trục Oy được gọi là trục giá trị của tang.
Trục Bs gốc B cùng hướng với trục Ox được gọi là trục giá trị của cotang.
– Giá trị lượng giác sin, cosin, tang và cotang:
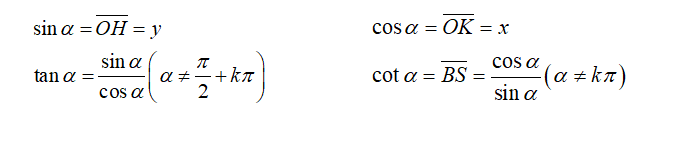
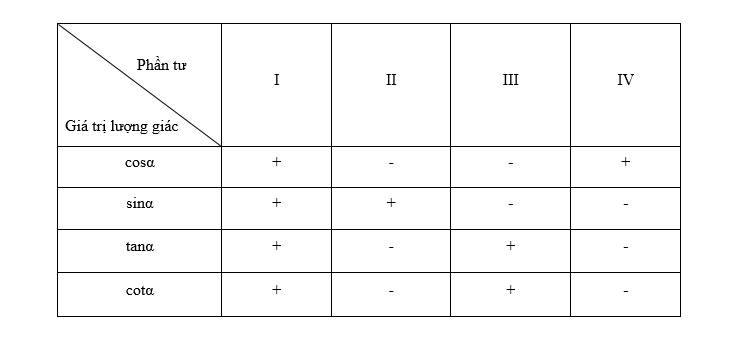
Dấu của các giá trị lượng giác
Cung liên kết- Phần kiến thức đường tròn lượng giác lớp 11 nhất định phải thuộc.
Góc đối nhau
( cos đối)
Góc bù nhau
(sin bù)
Góc phụ nhau
(Phụ chéo)
Góc hơn kém
(Khác pi tan)
cos (-α)= cos αSin (π-α) = sin αsin (π/2-α)= cos αSin (π+α) = -sin αSin (-α) = -sin αCos (π-α) – cos αcos (π/2-α) = sinαcos (π+α) = -cosαTan (-α) = tan αTan (π-α)= -tan αTan (π/2-α) = cot αtan (π+α) = tanαcot (-α) = -cot αcota (π-α)= – cot αCot (π/2-α) = tan αcot (π+α) = cotα
Trên đây là những kiến thức cơ bản nhất của đường tròn lượng giác lớp 11. Lượng kiến thức không nhiều nhưng học sinh cần phải nắm thật chắc các đinh lý, hệ quả, tính chất… để vận dụng làm bài tập.
Ngoài ra học sinh cũng cần phải nằm lòng một số công thức lượng giác quan trọng như: Công thức cộng, công thức nhân đôi, công thức hạ bậc, biến đổi tổng thành tích, tích thành tổng…
Tất cả những công thức này sẽ hỗ trợ các em giải các dạng toán như phương trình, hàm số lượng giác lớp 11…
Các công thức lượng giác trọng tâm
– Công thức cơ bản
Sin2x + cos2x =1Tanx = sinx/cosxCotx = cosx/sinxTanx.cotx = 11+tan2x = 1/ cos2x1 + cot2x = 1/sin2x
Công thức cộng
Cos (a+b) = cosa.cosb – sina.sinb
Cos (a-b) = cosacosb + sina.sinb
Sin (a+b) = sina.cosb + sinb.cosa
tan (a+b) = (tana + tanb)/ (1 – tana.tanb)
tan (a-b) = (tana – tanb)/ (1 + tana.tanb)
Công thức nhân đôi, hạ bậc
Trong bài đường tròn lượng giác lớp 11 thì công thức cộng, nhân đôi hạ bậc là hai phần đặt biệt quan trọng. Nếu không ghi nhớ được 2 phần kiến thức này, các em sẽ gặp nhiều khó khăn khi giải toán lượng giác và thậm chí là không giải được. Vậy nên ngay từ bây giờ cần tổng ôn các công thức này bằng cách thực hành bài tập thường xuyên.
Sin2a = 2sina.cosa, tan 2a = 2tana/(1 – tan²a)
Cos2a = 2cos²a – 1 = 1 – 2sin²a = cos²a – sin²a
Sin²a = (1-cos2a)/2, cos²a = (1+ cos2a)/2
Cos3a = 4cos³a – 3cosa ⇒ cos³a = (3cosa + cos3a) / 4
Sin3a = 3sina – 4sin³a ⇒ sin³a = (3sina -sin3a)/4
Công thức biến đổi tổng thành tích
Cosa + cosb = 2cos (a+b)/2.cos (a-b)/2
Cosa – cosb = -2sin(a+b)2.sin (a-b)/2.
Sina+sinb = 2sin(a+b)/2.cos (a-b)/2
Công thức biến đổi tích thành tổng
Cosa.cosb = 1/2 [cos (a-b) +cos (a+b)]
Sina.sinb = 1/2 [cos(a-b)- cos(a+b)]
Sina.cosb = 1/2 [ sin (a-b) + sin (a+b)].
CCBook đã tổng hợp lại tất tần tật những công thức liên quan đến đường tròn lượng giác lớp 11. Các em nên chăm chỉ làm bài tập để ghi nhớ kiến thức, đồng thời rèn sự phản xạ khi gặp các dạng bài phức tạp cần biến đổi.
Xem thêm: Cách dùng “vũ khí casio” diệt gọn câu hỏi hàm số lượng giác lớp 11 bài 1
Sách giúp cô đọng toàn bộ kiến thức lớp 11

Sách tổng hợp kiến thức trọng tâm và phân dạng bài tập đầy đủ thi THPT Quốc gia
Bên cạnh kiến thức về đường tròn lượng giác lớp 11, học sinh cũng cần chú ý đến chuyên đề phương trình lượng giác lớp 11, hàm số lượng giác. Đây đều là những phần rất hay xuất hiện trong đề thi THPT Quốc gia.
Các em nên hệ thống các phần kiến thức quan trọng ngay từ bây giờ để tiết kiệm thời gian ôn tập sau này. CCBook xin giới thiệu cuốn sách Đột phá 8+ kì thi THPT Quốc gia môn Toán- Đại số & giải tích. Sách sẽ giúp em cô đọng lại toàn bộ kiến thức và bài tập trọng tâm của lớp 11. Không chỉ có kiến thức lớp 11 mà còn có kiến thức lớp 10, 12.
Đây là cuốn sách luyện thi THPT Quốc gia môn Toán đầu tiên trình bày đầy đủ kiến thức 3 năm. Học sinh học đến đâu, hiểu đến đó vì lý thuyết và bài tập được trình bày song song.
Trong năm học cuối cấp, thì cuốn sách luyện thi THPT quốc gia này chắc chắn sẽ là một trợ thủ đắc lực giúp teen 2K1 nâng cao hiệu quả học tập.
