Bigdatauni.com Follow Fanpage Contact
Các bài viết trước chúng ta đã tìm hiểu thế nào là Time series, các ứng dụng trong lĩnh vực kinh tế, các chỉ số mô tả đối tượng nghiên cứu trong dữ liệu Time series, phương pháp Moving Average (Trung bình trượt) trong phân tích xu hướng biến động, đặc biệt trong phần 3 vừa rồi BigDataUni đã trình bày đến các bạn cách thức sử dụng Moving Average để phân tích các thành phần trong Time series, và hàm xu thế tuyến tính (Liner trend model) cho mục đích dự báo trong tương lai có điều chỉnh theo yếu tố thời vụ.
Đến với phần 4 của chuỗi các bài viết về Time series (phân tích chuỗi thời gian), chúng ta sẽ tìm hiểu đến 2 phương pháp phân tích Time series và dự báo được ứng dụng phổ biến trong lĩnh vực kinh doanh là Exponential Smoothing (dạng Simple và Holt-Winters).
Các bạn nào chưa biết gì về Time series có thể tham khảo các bài viết của chúng tôi tại các link dưới đây, chúng tôi sẽ không nói lại nội dung đã trình bày:
Tổng quan về Time series (chuỗi thời gian) (P.1) – Giới thiệu chung, ứng dụng, các thành phần Time series
Tổng quan về Time series (chuỗi thời gian) (P.2) – Các chỉ số mô tả đối tượng trong Time series, giới thiệu về Moving Average
Tổng quan về Time series (chuỗi thời gian) (P.3) – Phân tích các thành phần trong Time series sử dụng Moving Average, và dự báo bằng hàm xu thế
Mô hình san bằng hàm mũ – Exponential Smoothing
Hàm xu thế tuyến tính (Linear trend model) chỉ áp dụng phù hợp cho dữ liệu Time series mà ở đó chúng ta đã phân tích được tính biến động theo xu hướng, hay kết luận có tính xu hướng. Tuy nhiên nếu dữ liệu không hề có xu hướng thì khi dùng hàm xu thế để dự báo kết quả dĩ nhiên sẽ không chính xác.
Bên trên là công thức tổng quan của hàm xu thế, vậy câu hỏi đặt ra là khi hệ số B1 > 0, tức khi thời gian càng về xa, t lớn, thì giá trị dự báo cho Y sẽ tăng lên theo, B1 < 0, tức khi thời gian càng về xa, t lớn, thì giá trị dự báo cho Y sẽ giảm theo. Nhưng khi B1 gần tiến đến 0, không có mối quan hệ giữa Y và t thì t lớn, chúng ta không giải thích được Y trong tương lai sẽ tăng hay giảm.
Ở bài viết trước khi nói về trung bình trượt Moving Average, chúng ta đã biết Moving Average giúp loại bỏ các yếu tố ngẫu nhiên tác động lên đối tượng nghiên cứu, để giúp chúng ta nhìn ra rõ hơn xu hướng biến động. Tuy nhiên trung bình trượt không hỗ trợ dự báo, vì nếu thực sự có xu hướng, thì nó luôn mang lại giá trị dự báo “bị trễ” so với thực tế. Giải thích lại cho những bạn chưa biết:
Tại thời điểm Q3 – 2015, Net profit margin của McDonald’s cho thấy dấu hiệu tăng lên nhưng đến Q1-2016, thì đường MA – Trailing mới cho thấy xu hướng tăng này. Tuy việc dự báo trễ Net profit margin không gây thiệt hại gì cho McDonald’s nếu họ đưa vô áp dụng thực tế, nhưng giả sử ở các lĩnh vực khác việc dự báo trễ sẽ đem lại hậu quả to lớn ví dụ trong lĩnh vực Trading hay đầu tư tài chính, các chuyên gia thường không sử dụng MA đơn giản mà họ sử dụng các công cụ chỉ báo kết hợp MA phức tạp hơn nguyên nhân là do độ trễ trong dự báo của MA thường khiến họ chậm nhịp và bị tổn thất về mặt lợi nhuận.
Mặc dù Moving Average không thích hợp để hỗ trợ dự báo, và kể cả khi nó không giúp chúng ta nhìn thấy được tính thời vụ của Time series trên biểu đồ, thì trung bình trượt vẫn là công cụ đắc lực trong việc phân tích từng thành phần trong Time series, đặc biệt là giúp xác định chỉ số thời vụ và loại bỏ chính yếu tố thời vụ, xác định hàm xu thế và loại bỏ yếu tố xu hướng khi cần thiết,…
Do đó ngay cả trong các phương pháp sau này BigDataUni trình bày như Exponential Smoothing trong bài viết này hay ARIMA ở bài viết tới đều có đề cập đến Moving Average.
Quay trở lại với Exponential Smoothing, thì đây là công cụ giúp chúng ta linh hoạt phân tích và dự báo trong Time series áp dụng cho cả dữ liệu có hay không có yếu tố xu hướng và thời vụ. Chính vì ưu điểm này, nó được ứng dụng phổ biến thứ 2 sau mô hình ARIMA.
Chúng ta cùng đi vào dạng đầu tiên Simple Exponential Smoothing.
Simple Exponential Smoothing
San bằng hàm mũ đơn giản thực chất dựa trên triết lý vận hành của Moving average đó là sử dụng những giá trị trong quá khứ rồi san phẳng để loại bỏ yếu tố ngẫu nhiên bất thường để hỗ trợ phân tích và dự báo tuy nhiên chỉ khác ở chỗ chúng ta sẽ không tính trung bình trượt với bất kỳ mức k nào cả thay vào đó sẽ sử dụng trung bình có trọng số áp dụng cho tất cả giá trị trong quá khứ.
Khác với Moving Average, tất cả các giá trị quá khứ đều có sự tác động như nhau đối với việc dự báo cho đối tượng nghiên cứu, thì trong Simple Exponential Smoothing, những giá trị ở các mốc thời gian khác nhau sẽ được đánh giá mức độ ảnh hưởng, và tầm quan trọng khác nhau. Trong đó, những giá trị có mốc thời gian gần hơn với mốc thời gian cần dự báo thì sẽ được đánh trọng số cao hơn các giá trị lùi xa về quá khứ.
Hiểu đơn giản, nếu giả sử không có tác động của những yếu tố ngẫu nhiên thì thông tin mới nhất sẽ hỗ trợ rất nhiều cho việc dự báo. Ví dụ doanh thu quý 2, quý 3 của McDonald’s sẽ có thể giúp dự báo cho doanh thu quý 4 trong năm giả định không có các yếu tố ngẫu nhiên mạnh, lúc này trọng số sẽ điều chính ở giá trị cao.
Simple Exponential Smoothing cũng khác với Moving Average dạng Weighted, đó là chỉ sử dụng 1 trọng số duy nhất cho các giá trị có mốc thời gian gần nhất.
Khi chưa tính đến so sánh kết quả phân tích giữa các phương pháp, thì san bằng hàm mũ đơn giản cho thấy hiệu quả hơn khi nó sử dụng 100% giá trị đầu vào, còn Moving Average chúng ta không thể sử dụng hết 100% khi phải loại bỏ các giá trị không tính được trung bình trượt.
Simple Exponentail Smoothing thích hợp để áp dụng cho dữ liệu đã bị loại bỏ yếu tố xu hướng và thời vụ, sử dụng Moving Average giống ở bài viết trước.
Tại một mốc thời gian t cụ thể, chúng ta sẽ dùng các giá trị trước đó, quá khứ để ước lượng và dùng chính giá trị ước lượng cho t này để dự báo các mốc thời gian trong tương lai (t + 1), (t + 2)
Nói cách khác là nhìn lại giá trị dự báo tại mốc t trước đó so sánh với giá trị thực tế tại t để xem xét sai số, lấy đó làm “bài học” để dự báo các mốc thời gian trong tương lai.
San bằng hàm mũ đơn giản giúp chúng ta chủ động hơn trong quá trình phân tích, có thể sử dụng kinh nghiệm, kiến thức, am hiểu về đối tượng để tinh chỉnh mô hình sao cho mang lại kết quả dự báo chính xác như mong đợi.
Công thức tổng quát
Ft+1 = αYt + (1 – α)Ft
Với Ft+1 là giá trị dự báo tại mốc thời gian t + 1; Ft là giá trị dự báo ở mốc thời gian t, Yt là giá trị thực tế ở thời điểm t, và α là hằng số san bằng mũ hay được gọi là trọng số.
Để dự báo cho F2, giả sử kết quả dự báo F1 = Y1 (do khi dự báo F2 chúng ta đã có được giá trị thực tế tại t = 1) chúng ta sẽ có:
F2 = αY1 + (1 – α)F1 = αY1 + (1 – α)Y1 = Y1
Tương tự cho F3 và F4
F3 = αY2 + (1 – α)F2 = αY2 + (1 – α)Y1
F4 = αY3 + (1 – α)F3 = αY3 + (1 – α)[ αY2 + (1 – α)Y1] = αY3 + α (1 – α)Y2 + (1 – α)2Y1
Các bạn có thể thấy để dự báo cho mốc thời gian F4 chúng ta sẽ lấy trung bình có trọng số của các giá trị trong quá khứ, mốc thời gian càng gần thì trọng số càng lớn và ngược lại. Tổng trọng số cộng lại sẽ bằng 1.
Việc quan trọng là xác định trọng số α từ 0 đến 1 sao cho đạt được két quả dự báo như mong đợi.
Các cách chọn trọng số:
- Dựa trên kinh nghiệm phân tích, sự am hiểu về đối tượng nghiên cứu cũng như các yếu tố tác động đến nó đã biết từ trước đó. Ví dụ các nhà phân tích biết được các giá trị ở quá khứ gần hơn thường giúp ích nhiều cho việc dự báo nên sẽ đánh trọng số cao và ngược lại
- Dựa trên sai số dự báo, trọng số nào có sai số dự báo thấp nhất sẽ được chọn. Cách đánh giá dựa trên so sánh các chỉ tiêu MAE, MSE, RMSE, MAPE mà chúng tôi có nhắc đến ở phần 3
- Dựa vào tính biến động, mức độ tác động của yếu tố ngẫu nhiên không thể kiểm soát. Ví dụ sau khi loại bỏ yếu tố thời vụ, yếu tố xu hướng mà dữ liệu Time series chưa thực sự bằng phẳng (nhìn trên đồ thị) thì không thể đặt trọng số quá cao cho các giá trị quá khứ ở mốc thời gian gần với mốc dự báo, và ngược lại nếu dữ liệu có vẻ bằng phẳng hơn.
Quay trở lại với công thức đầu tiên chúng ta có:
Ft+1 = αYt + (1 – α)Ft
Ft+1 = Ft + α(Yt – Ft)
Giá trị dự báo tại thời điểm t+1 sẽ lấy giá trị dự báo tại mốc t sau đó điều chỉnh lại dựa trên thông tin về sai số dự báo bằng cách thêm vào trọng số phù hợp. Nếu các yếu tố ngẫu nhiên tác động mạnh thì sai số (Yt – Ft) sẽ lớn, nên chọn α nhỏ và ngược lại.
Đó là giải thích dấu chấm thứ 3 ở trên cho các bạn chưa hiểu.
Giờ chúng ta quay lại với ví dụ McDonald’s. Như đã nói ở trên, Simple Exponentail Smoothing thích hợp để áp dụng cho dữ liệu đã bị loại bỏ yếu tố xu hướng và thời vụ. Tuy nhiên để so sánh hiệu quả, giả sử dữ liệu sử dụng là dữ liệu gốc thì kết quả dự báo sẽ ra sao so với phương pháp hàm xu thế kết hợp loại bỏ yếu tố thời vụ đã đề cập ở bài viết trước.
Chúng ta thử nghiệm cả 3 trọng số trong đó α = 0.2; α = 0.5 và α = 0.8
Với α = 0.2 Đầu tiên chúng ta sẽ lấy F2 = Y1, như theo công thức chứng minh ở trên.
F3 = α*Y2 + (1 – α)*F2 = 0.2*6075 + (1 – 0.2)*5615 = 5707
F4 = α*Y3 + (1 – α)*F3 = 0.2*6267+ (1 – 0.2)*5707 = 5819
Các bạn tính tiếp tục cho đến F51. Sau đó tính trung bình sai số dự báo bình phương (Mean Squared Error) công thức
Chúng ta tiếp tục tính cho trường hợp α = 0.5, và 0.8
Chúng tôi cắt bớt độ dài bảng để tránh bài viết cồng kềnh
Như vậy trong 3 hệ số san bằng hàm mũ, chúng ta có thể thấy α = 0.5 có MSE thấp nhất, nên chúng ta có thể sử dụng để dự báo doanh thu quý 4 của McDonald’s
F52 = α*Y51 + (1 – α)*F51 = 5418*0.5 + (1 – 0.5)*4375.7 = 4896.85
Theo như trên thì quý 4 sắp tới McDonald’s có doanh thu dự báo 4.9 tỷ USD.
Nói đúng hơn thì để hệ số α chạy từ 0 đến 1 thì chắc chắn sẽ có một giá trị làm MSE nhỏ hơn cả α = 0.5, thậm chí nhỏ nhất.
Có một cách đó chính là dùng Solver – Excel ở phần Add-ins
Để thực hiện thì trước tiên các bạn phải lập bảng tính, xây dựng công thức cho cột Forecast, Forecast Error và SE^2 , và đặc biệt là ở MSE, rồi làm 1 ô vàng α mà chúng tôi tô vàng ở trên.
Các bạn vào Solver sẽ thấy bảng dưới đây, tại ô Set Objective cái bạn thêm vị trí ô MSE, của chúng tôi là F54 (cột F, dòng 54), By changing varibale cells là ô α, tiếp chúng ta tạo điều kiện cho hệ số, α chạy từ 0 đến 1. Để thêm điều kiện các bạn click vào Add, chọn ô α, rồi cứ thế làm.
Sau khi nhấn “Solve” các bạn sẽ thấy “Keep Solver Solution” tức giữ giá trị tối ưu của α vừa tìm được và bảng tính sẽ sử dụng luôn để tính MSE cho bạn.
Kết quả ví dụ trên, α tối ưu = 0.5024, không chênh lệch với 0.5 ở trên, và MSE nhỏ nhất sẽ bằng 182539.
Ở bài viết trước, sử dụng hàm xu để dự báo thì chúng ta có MSE = 403784, như vậy Simple Exponential Smoothing cho thấy độ hiệu quả hơn rất nhiều.
Holt-Winters exponential smoothing
Mô hình san bằng hàm mũ đơn giản đem lại kết quả dự báo ít chính xác nếu dữ liệu Time series thể hiện nó tính xu hướng, hay thời vụ. Khi đó các giá trị quá khứ gần hoặc ở xa mốc thời gian cần dự báo có sự ảnh hưởng ra sao là không thể xác định.
Đối với dữ liệu Time series có thành phần xu hướng, có cả xu hướng và thời vụ, hay chỉ có mỗi thành phần thời vụ, thì chúng ta có thể sử dụng phương pháp Holt – winters.
- Đối với dữ liệu Time series có xu hướng (Trend)
Đối với dữ liệu Time series có tính xu hướng chúng ta sử dụng 2 lần san bằng hàm mũ đơn giản. Chúng ta sẽ bắt đầu ước lượng giá trị của đối tượng nghiên cứu tại thời điểm t, tiếp tục ước lượng tiếp tác động của yếu tố xu hướng và sau cùng là dự báo.
Công thức như sau
Xt = αYt + (1 – α)(Xt-1 + Tt-1)
Giá trị ước lượng tại thời điểm t sẽ bằng trung bình có trọng số giá trị thực tế tại t (Yt) và giá trị ước lượng tại t-1 bao gồm thành phần xu hướng (Xt – 1+ Tt-1)
Tức khi có thành phần xu hướng thì cộng thêm phần điều chỉnh theo xu hướng nên cộng thêm Tt – 1 (đây là điểm khác với Simple Exponential Smoothing)
Tiếp theo cho khi dự báo cho các mốc t + 1, chúng ta phải ước lượng được thành phần xu hướng tại chính mốc thời gian t (Tt). Theo Holt-Winters nếu dữ liệu Time series có tính xu hướng thì sự khác biệt giữa 2 giá trị tại 2 mốc thời gian liền kề chính là do yếu tố xu hướng gây ra.
Do đó phần đầu tiên sẽ là (Xt – Xt-1), phần thứ 2 sẽ là Tt-1 nghĩa là Tt được dự báo dựa trên một phần thông tin từ Tt-1 ở mốc trước đó.
Tt = β(Xt – Xt-1) + (1 – β)Tt-1
Dự báo cho t, thì cần tìm Tt – 1 và đến t + 1 thì cần tìm Tt. Dễ hiểu đúng không?
Xt+1 = αYt+1 + (1 – α)(Xt + Tt)
Để dự báo Xt + 2 thì cần ước lượng:
Tt+1 = β(Xt+1 – Xt) + (1 – β)Tt
Trọng số thể hiện mức độ quan trọng hay tác động của thông tin quá khứ lên thông tin dự báo trong tương lai. Nếu Xt – 1 tác động nhiều lên việc dự báo Xt thì (1 – α) sẽ lớn, tức α sẽ nhỏ và ngược lại. Xét tương tự cho phần công thức xu hướng.
Sau cùng để dự báo cho các giá trị tương lai chúng ta sử dụng công thức:
Phương pháp của Holt-Winters cho thấy cách phân tích chủ động hơn hàm xu thế tuyến tính và san bằng hàm mũ đơn giản, nghĩa là khi có một giá trị quan sát mới, nó sẽ được dùng để ước lượng thành phần xu hướng để cập nhật, và sau đó dùng thông tin này để dự báo cho tương lai. Ví dụ các bạn thấy sau khi ước lượng được Xt rồi thì cần gì ước lượng thêm thành phần xu hướng của nó là Tt và đem Tt vào để dự báo cho Xt+1?
Điều quan trọng là xác định hệ số α, β sao cho sai số dự báo nhỏ nhất. Xem lại phần Simple ở trên nếu các bạn quên.
Chúng ta sẽ tiếp tục sử dụng Excel – Solver như trên để xác định hệ số tối ưu, và thử nghiệm.
Sau khi dùng Solver, chúng ta có α = 0.603 và β = 0.1806
Cách tính:
Đầu tiên cho X2 = Y2 = 6075, T2 = Y2 – Y1 = 6075 – 5615 = 460
Xt = αYt + (1 – α)(Xt-1 + Tt-1) => X3 = αY3 + (1 – α)(X2+ T2) = 0.603*6267 + (1 – 0.603)*(6075 + 460) = 6373.39
Tt = β(Xt – Xt-1) + (1 – β)Tt-1 => T3 = β(X3 – X2) + (1 – β)T2 = 0.1806*(6373.39 – 6075) + (1 – 0.1806)*460 = 430.81
Các bạn tính tiếp cho X4 và T4
Dự báo tại t = 3, F(X2 + 1 = 3)= X2 + 1*T2 = 6075 + 460 = 6535
F (X4) = X3 + T3 = 6373.39 + 430.82 = 6804.21
Các bạn có thể thấy MSE tại đây còn cao hơn MSE ở Simple Exponenetial Smoothing, suy ra kết quả dự báo ít chính xác, kém hiệu quả. Nghĩa là dữ liệu không thể hiện xu hướng quá rõ ràng, trong suốt khoảng thời gian, doanh thu của McDonald’s có tăng dần và giảm dần ở một số thời điểm (thành phần T được định lượng ở trên bảng không cho thấy dữ liệu tăng đều hay giảm đều qua thời gian, chúng giảm rồi lại tăng và ngược lại)
Giả định thứ 2, chính là do dữ liệu có yếu tố mùa vụ tác động khiến thành phần xu hướng bị biến động. Trước khi sang phần cuối cùng. Chúng ta cùng dự báo thử cho Q4-2020, Q1-2021
Q4 – 2020 tức t = 52, lúc này không có giá trị thực tại Q4, nên chúng ta không thể tìm thành phần X và T, nên sử dụng công thức dự báo ở trên:
F52 = X51 + 1*T51 = 5418 + (-46.11) = 5371.89
F53 = X51 + 2*T51 = 5418 + 2*(-46.11) = 5325.78
Như vậy thời gian càng xa trong tương lai, thì giá trị dự báo sẽ càng giảm, điều này chắc chắn vô lý nếu dữ liệu doanh thu Mc.Donald’s thực sự không có tính xu hướng và ngược lại. Nói đơn giản làm sao doanh thu cảu Mc.Donald’s giảm hoài được!
Kết quả dự báo chỉ hợp lý khi dữ liệu có tính xu hướng, hay nói cách khác, loại trừ bất kể tác động gì xảy đến, doanh thu Mc.Donald’s sẽ càng tăng lên theo thời gian (T sẽ tăng từ t = 1 đến t =51). Điều này có thể xảy ra nếu hàng năm Mc.Donald’s tăng đầu tư, mở rộng kinh doanh qua các năm.
- Đối với dữ liệu có tính xu hướng và cả tính thời vụ
Tương tự như ở dữ liệu có tính xu hướng, chúng ta thêm thành phần xu hướng và gán trọng số cho nó để chuyển thành trung bình có trọng số. Cách xác định trọng số cũng tương tự như ở các phương pháp trên.
Ở phương pháp Holt-Winters, ngay ở công thức đầu tiên, chúng ta phải điều chỉnh giá trị ước lượng Xt thêm thành phần xu hướng, thì ở đây, chúng ta tiếp tục điều chỉnh thêm thành phần thời vụ bằng cách lấy Yt/ St – m
Xt = αYt/ St – m + (1 – α)(Xt-1 + Tt-1)
m là số kỳ trong thời vụ, tức quý thì có 4 tháng, m = 4, một thời vụ có 12 tháng thì m = 12
St – m là giá trị ước lượng cho chỉ số thời vụ. Tiếp theo ước lượng thành phần xu hướng T y chang ở trên
Tt = β(Xt – Xt-1) + (1 – β)Tt-1
Sau cùng ước lượng chỉ số thời vụ S tại thời điểm t, St = Yt/ Tt (xem lại mô hình nhân, và phần phân tích thành phần Time series ở các bài viết trước) tức đã điều chỉnh thành phần xu hướng và dựa trên thông tin của St – m tìm được.
St = γYt/ Xt + (1 – γ)St – m
Hệ số γ cũng có chức năng tương tự như α, β nên chúng tôi không nói lại.
Chúng ta phải xác định các giá trị khởi đầu cho việc tính toán như X2, T2 ở phương pháp vừa rồi.
Chúng ta sẽ tìm các giá trị ban đầu cho S, T, X
Đầu tiên tính trung bình trượt 4 mức độ và trung bình trượt 2 mức độ do dữ liệu doanh thu Mc.Donald’s theo quý, mỗi năm có 4 quý. Lý do tại sao tính 2 lần trung bình trượt cá bạn xem lại bài viết phần 2, và 3 nhé!
Cách chọn S, T, X như sau:
X5m/2= Y**5m/2
T5m/2 = Y**5m/2 – Y**(5m/2) – 1
S(5m/2) – j = (1/2) [(Y(5m/2) – j / Y**(5m/2) – j) + (Y(3m/2) – j / Y**(3m/2) – j)]
j = 0, 1, 2, 3,… m – 1. Vì m = 4, vậy j = {0, 1, 2, 3}. Chúng ta có thể xác định trước S10, S9, S8, S7.
Vì m = 4, X10 = Y**10
T10 = Y**10 – Y**9
S7 = (1/2)[(Y7/ Y**7) + (Y3/ Y**3)] Các bạn xét tương tự cho S8, S9, S10
Sử dụng Solver – Excel, để tìm các hằng số. Chúng ta có bảng sau, lưu ý (Revenue = y)
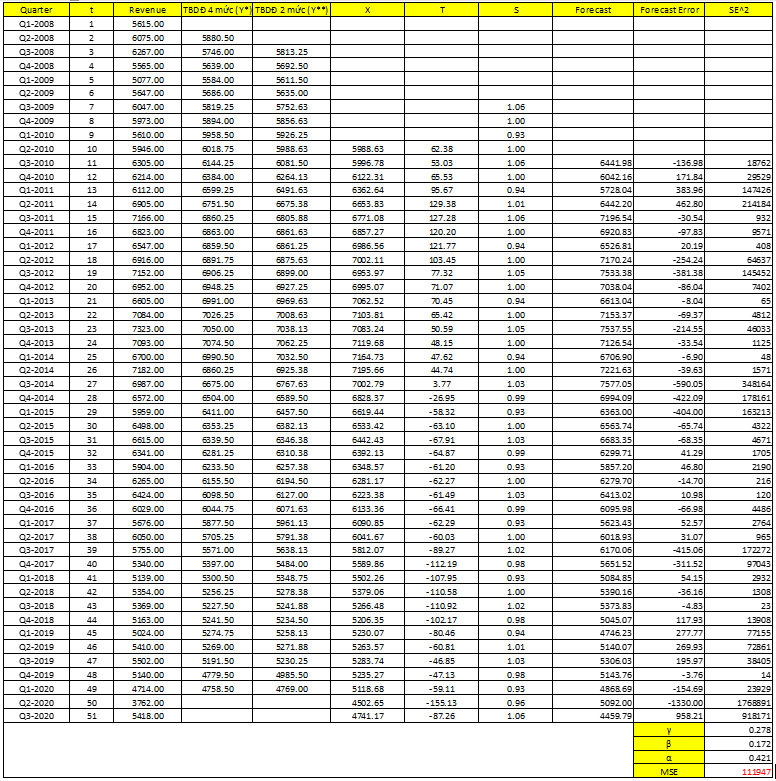
X10 = 5988.63; T10 = 6081.5 – 5988.63 = 62.38; S7 = 1.06
X11 = (0.421*Y11)/ S7 + (1 – 0.421)*(X10 + T10) = 5996.78
T11 = 0.172 (X11 – X10) + (1 – 0.172)*T10 = 53.03
S11 = 0.278*(Y11/ X11) + (1 – 0.278)*S7 = 1.06
Các bạn tính tiếp tục cho các giá trị tiếp theo.
Để dự báo chúng ta sử dụng công thức:
Fn + h = (Xn + h*Tn)*Sn+h-m
F11 = (X10 + 1*T10)*S10+1-4 = 6441.98
Còn để dự báo cho Quý 4 – 2020, Quý 1 – 2021:
F52 = (X51 + 1*T51)*S51+1-4 = (X51 + T51)*S48 = (4741.17 – 87.26)*0.98 = 4560.8
F53 = (X51 + 2*T51)*S51+2-4 = (X51 + 2*T51)*S49 = (4741.17 – 2*87.26)*0.93 = 4246.9
Chúng ta nhìn vào MSE = 111947 là giá trị thấp nhất trong tất cả các phương pháp được sử dụng, chứng tỏ chúng ta cần áp dụng phương pháp san bằng hàm mũ dành cho dữ liệu xu hướng kết hợp thời vụ. Như vậy cũng kết luận dữ liệu Time series có cả tính thời vụ và xu hướng.
Tài liệu tham khảo
“Statistics for Business and Economics” của tác giả Paul Newbold, William L. Carlson, Betty M. Thorne
“The Practice of Statistics for Business and Economics” của tác giả David S. Moore và cộng sự
“PROBABILITY and STATISTICS for FINANCE” của tác giả Svetlozar (Zari) T. Rachev và cộng sự
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.
