Trong Toán học, ta rất dễ gặp các dạng bài tập tính hệ số góc. Ngoài ra, hệ số góc còn được vận dụng rất nhiều vào đời sống thực tiễn. Vậy hệ số góc là gì? Làm thế nào để tính hệ số góc trong các trường hợp? Bài viết dưới sẽ giúp bạn giải đáp những thắc mắc trên. Hãy cùng chúng mình tìm hiểu rõ hơn nhé!
Hệ số góc là gì? Khái niệm hệ số góc
Hệ số góc là một thuật ngữ phổ biến trong Toán học. Khi xét hệ số góc, ta thường xét nó trên một đường thẳng. Chính vì vậy, hệ số góc còn được gọi một cách đầy đủ là hệ số góc của đường thẳng.
Hệ số góc chính là độ dốc của một đường thẳng bất kỳ. Giá trị của hệ số góc càng lớn thì độ dốc càng lớn. Ngoài ra, ta cũng có thể xét đến trường hợp mặt phẳng Oxy, đường thẳng a tạo với trục 0x một góc α. Hệ số góc của đường thẳng a chính là tan α. Nếu đường thẳng a vuông góc với Ox thì nó không có hệ số góc.
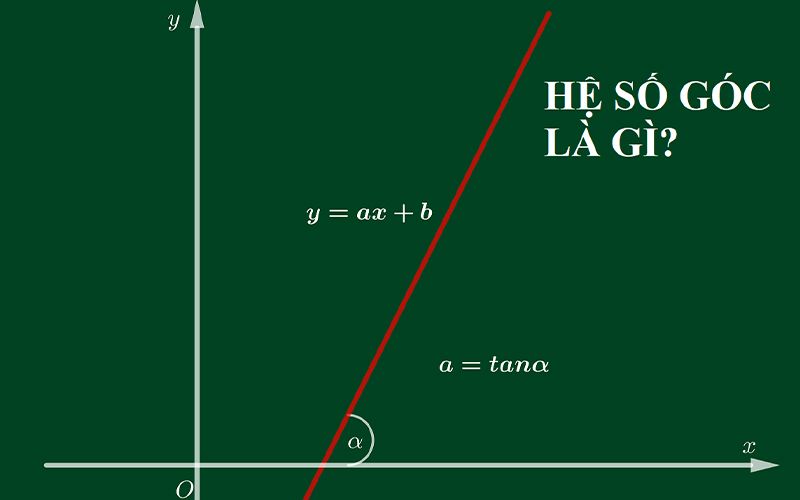
Cách tính hệ số góc
Chúng ta sẽ xét hệ số góc đối với các loại đường thẳng gồm tiếp tuyến, y = ax + b và hệ số góc k.
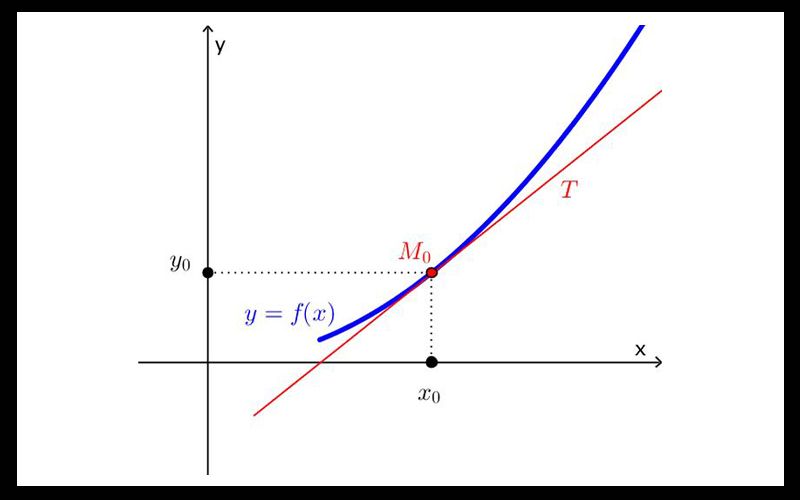
Cách tính hệ số góc của tiếp tuyến
Trong trường hợp này, đề bài sẽ đưa ra dữ liệu tiếp tuyến với một đồ thị hàm số tại một điểm có hoành độ x = a. Để tính hệ số góc của tiếp tuyến, ta thực hiện theo các bước sau đây:
- Đạo hàm hàm số đã cho
- Thay x = a vào phần đạo hàm của hàm số. Kết quả thu được chính là hệ số góc cần tìm
Cách tính hệ số góc k
Hệ số k phụ thuộc vào đường thẳng và mặt phẳng Oxy đã cho. Tùy thuộc vào từng dữ liệu mà đề bài đưa ra, ta sẽ lần lượt thay các dữ liệu này vào đường thẳng a để tìm ra hệ số góc k. Kết quả cuối cùng mà ta tìm được chính là hệ số góc k.
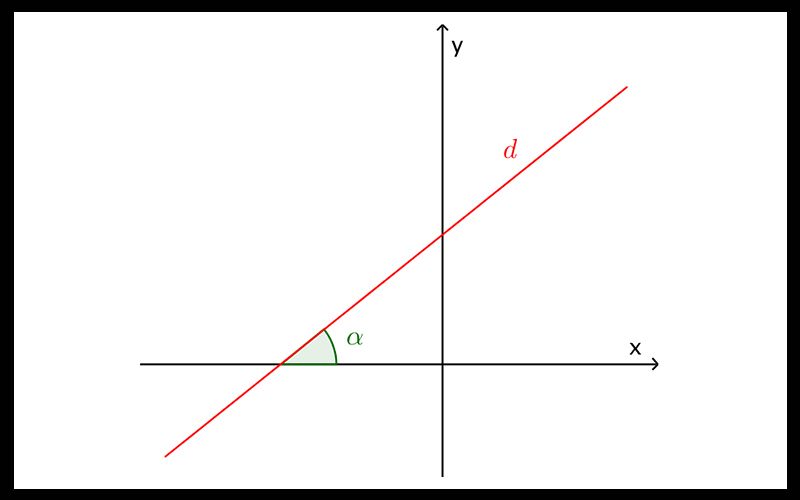
Cách tính hệ số góc của đường thẳng
Một đường thẳng d bất kỳ sẽ được viết dưới dạng công thức tổng quát là: Ax + By + C = 0 (với B ≠ 0).
Khi đó, ta sẽ chuyển hệ số góc của đường thẳng d thành hệ số góc của đường thẳng y = ax + b.
Khi đó ta có: A/Bx + y + C/B=0
⇒ y = − A/Bx − C/B
Hệ số góc của đường thẳng d mà ta cần tìm chính là k = −A/B
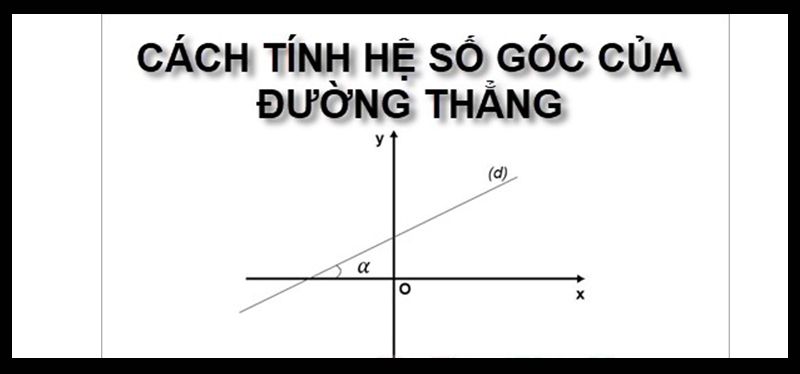
Cách tính hệ số góc của đường thẳng y = ax + b
Để tính hệ số góc của đường thẳng y = ax + b với mặt phẳng Oxy, ta sẽ xét một số trường hợp dưới đây:
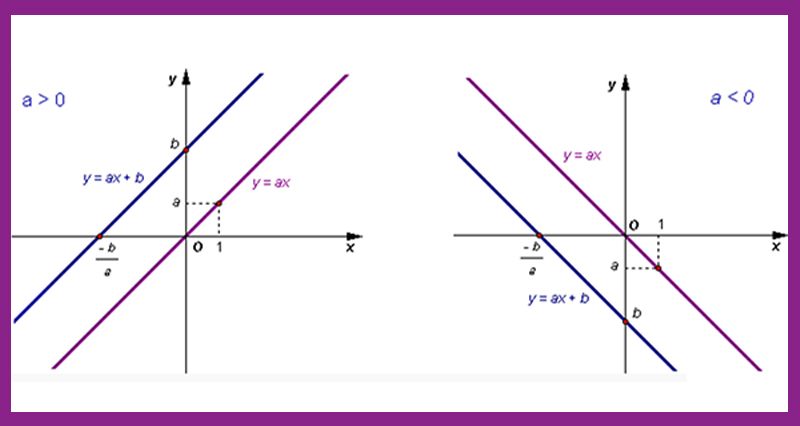
- Trường hợp a > 0: Góc được tạo bởi đường thẳng y = ax + b và trục Ox của mặt phẳng Oxy là một góc nhọn. Hệ số a càng lớn thì góc này vẫn sẽ nhỏ hơn 90°
- Trường hợp a < 0: Góc được tạo bởi đường thẳng y = ax + b và trục Ox của mặt phẳng Oxy là một góc tù. Dù hệ số a càng lớn thì góc này vẫn sẽ nhỏ hơn 180°
Lúc này, hệ số a chính là hệ số góc của đường thẳng y = ax + b với mặt phẳng Oxy.
Bài tập về hệ số góc
Dưới đây là một số bài tập vận dụng về hệ số góc. Mời các bạn cùng tham khảo.
- Bài tập 1: Phát biểu nào dưới đây là sai?
A. Góc được tạo bởi đường thẳng y = ax + b và trục Ox của mặt phẳng Oxy phụ thuộc vào a
B. Hệ số góc của đường thẳng y = ax + b là b
C. Hệ số góc cho ta biết độ dốc của một đường thẳng
D. Hệ số góc càng lớn thì độ dốc của đường thẳng càng lớn
Đáp án: B
- Bài tập 2: Chọn đáp án đúng trong các phát biểu dưới đây:
A. Cho đường thẳng y = ax + b, nếu a > 0 thì góc được tạo bởi đường thẳng y = ax + b và trục Ox là một góc nhọn
B. Cho đường thẳng y = ax + b, nếu a > 0 thì góc được tạo bởi đường thẳng y = ax + b và trục Ox là một góc tù
C. Cho đường thẳng y = ax + b, nếu a > 0 thì góc được tạo bởi đường thẳng y = ax + b và trục Ox là một góc vuông
D. Cho đường thẳng y = ax + b, nếu a < 0 thì góc được tạo bởi đường thẳng y = ax + b và trục Ox là một góc nhọn
Đáp án: A
- Bài tập 3: Cho đường thẳng (d): 2y – x + 1 = 0. Tính:
a. Hệ số góc của đường thẳng (d)?
b. Góc được tạo bởi đường thẳng (d) cùng chiều dương của trục Ox?
Đáp án:
a. Ta có: 2y – x + 1 = 0
⇔ 2y = x−1
⇔ y = 1/2x − 1/2
Vậy hệ số góc của đường thẳng (d): 2y – x + 1 = 0 là a = 1/2
b. Gọi α là góc được tạo bởi đường thẳng (d) cùng chiều dương của trục Ox.
Vì tan α = a = 1/2 => α = arctan 1/2
- Bài tập 4: Cho hàm số y = ax + 3. Tìm hệ số góc a, biết rằng đồ thị của hàm số trên đi qua điểm A(2; 6).
Đáp án:
Hy vọng bài viết trên đã giúp các bạn hiểu rõ hơn về hệ số góc, cũng như nắm được một số dạng bài tập liên quan. Chúc các bạn sẽ gặt hái được kết quả cao những kỳ thi quan trọng.
