Định nghĩa tập hợp hữu hạn
Tập hợp hữu hạn là tập hợp có số phần tử hữu hạn / đếm được. Tập hợp hữu hạn còn được gọi là tập hợp đếm được vì chúng có thể đếm được. Quá trình sẽ hết phần tử để liệt kê nếu các phần tử của tập hợp này có số phần tử hữu hạn.
Ví dụ về tập hợp hữu hạn:
P = {0, 3, 6, 9,…, 99}
Q = {a: a là số nguyên, 1 <a <10}
Một tập hợp tất cả các Bảng chữ cái tiếng Anh (vì nó có thể đếm được).
Một ví dụ khác về tập hợp hữu hạn:
Một tập hợp các tháng trong một năm.M = {tháng 1, tháng 2, tháng 3, tháng 4, tháng 5, tháng 6, tháng 7, tháng 8, tháng 9, tháng 10, tháng 11, tháng 12}
n (M) = 12
Nó là một tập hợp hữu hạn vì số phần tử có thể đếm được.
Cardinality của tập hợp hữu hạn
Nếu ‘a’ đại diện cho số phần tử của tập A, thì tổng số của một tập hữu hạn là n (A) = a .
Vì vậy, Cardinality của tập hợp A của tất cả các bảng chữ cái tiếng Anh là 26, vì số phần tử (bảng chữ cái) là 26.
Do đó, n (A) = 26.
Tương tự, đối với một tập hợp chứa các tháng trong năm sẽ có số lượng là 12.
Vì vậy, theo cách này, chúng ta có thể liệt kê tất cả các phần tử của bất kỳ tập hợp hữu hạn nào và liệt kê chúng trong dấu ngoặc nhọn hoặc ở dạng Danh sách.
Thuộc tính của tập hợp hữu hạn
Các điều kiện tập hợp hữu hạn sau luôn luôn hữu hạn.
- Một tập hợp con của tập hợp hữu hạn
- Hợp của hai tập hợp hữu hạn
- Tập hợp lũy thừa của một tập hợp hữu hạn
Một vài ví dụ:
P = {1, 2, 3, 4}
Q = {2, 4, 6, 8}
R = {2, 3)
- Ở đây, tất cả P, Q, R là các tập hữu hạn vì các phần tử là hữu hạn và có thể đếm được.
- R ⊂ P, tức là R là Tập con của P vì tất cả các phần tử của tập R đều có trong P. Vì vậy, tập con của một tập hữu hạn luôn hữu hạn.
- PUQ là {1, 2, 3, 4, 6, 8}, do đó hợp của hai tập hợp cũng hữu hạn.
Số phần tử của một tập hợp lũy thừa = 2 n .
Số phần tử của tập hợp lũy thừa của tập P là 2 4 = 16, vì số phần tử của tập hợp P là 4. Vậy chứng tỏ rằng tập hợp lũy thừa của một tập hợp hữu hạn là hữu hạn.
Tập hợp hữu hạn không rỗng
Nó là một tập hợp mà số lượng phần tử lớn hoặc chỉ bắt đầu hoặc kết thúc được đưa ra. Vì vậy, chúng tôi ký hiệu nó với số phần tử với n (A) và nếu n (A) là một số tự nhiên thì nó là một tập hợp hữu hạn.
Ví dụ :
S = {tập hợp số người sống ở Ấn Độ}
Rất khó để tính toán số người sống ở Ấn Độ nhưng ở đâu đó nó là một con số tự nhiên. Vì vậy, chúng ta có thể gọi nó là một tập hữu hạn không rỗng.
Nếu N là tập hợp các số tự nhiên nhỏ hơn n. Vì vậy, bản số của tập N là n.
N = {1,2,3… .n}
X = x 1 , x 2 , ……, x n
Y = {x: x 1 ϵ N, 1 ≤ i ≤ n}, trong đó i là số nguyên từ 1 đến n.
Chúng ta có thể nói rằng một tập hợp rỗng là một tập hợp hữu hạn không?
Trước tiên chúng ta hãy tìm hiểu tập hợp rỗng là gì.
Tập hợp rỗng là tập hợp không có phần tử nào trong đó và có thể được biểu diễn dưới dạng {} và cho thấy rằng nó không có phần tử.
P = {} Hoặc ∅
Vì tập hữu hạn có số phần tử đếm được và tập rỗng không có phần tử nào nên nó là một số phần tử xác định.
Vì vậy, với một số 0, một tập hợp rỗng là một tập hợp hữu hạn.
Tập hợp Infinite là gì?
Nếu một tập hợp không hữu hạn, nó được gọi là tập hợp vô hạn vì số phần tử trong tập hợp đó là không thể đếm được và chúng ta cũng không thể biểu diễn nó dưới dạng danh sách. Vì vậy, tập hợp vô hạn còn được gọi là tập hợp không đếm được .
Vì vậy, các phần tử của một tập hợp Vô hạn được biểu diễn bằng 3 dấu chấm (hình elip), do đó, nó thể hiện tính vô hạn của tập hợp đó.
Ví dụ về Bộ vô hạn
- Tập hợp tất cả các số nguyên, W = {0, 1, 2, 3, 4,…}
- Tập hợp tất cả các điểm trên một đường thẳng
- Tập hợp tất cả các số nguyên
Số lượng bộ vô hạn
Tổng số của một tập hợp là n (A) = x, trong đó x là số phần tử của một tập hợp A. Tính tổng số của một tập hợp vô hạn là n (A) = ∞ vì số phần tử trong đó là không giới hạn.
Thuộc tính của tập hợp vô hạn
- Hợp của hai tập hợp vô hạn là vô hạn
- Tập hợp lũy thừa của một tập hợp vô hạn là vô hạn
- Siêu tập của một tập hợp vô hạn cũng là vô hạn
So sánh các tập hợp hữu hạn và vô hạn:
Hãy so sánh sự khác biệt giữa tập hữu hạn và tập hợp vô hạn:
Các tập hợp chỉ có thể bằng nhau nếu các phần tử của chúng giống nhau, vì vậy một tập hợp chỉ có thể bằng nhau nếu nó là một tập hợp hữu hạn, trong khi nếu các phần tử không thể so sánh được thì tập hợp là vô hạn.
Làm thế nào để biết một Tập hợp là Hữu hạn hay Vô hạn?
Như chúng ta biết rằng nếu một tập hợp có cả điểm bắt đầu và điểm kết thúc thì nó là một tập hợp hữu hạn, nhưng nó là vô hạn nếu nó không có điểm kết thúc từ bất kỳ phía nào hoặc cả hai phía.
Các điểm để xác định một tập hợp là hữu hạn hay vô hạn là:
- Một tập hợp vô hạn là vô tận từ đầu hoặc cuối, nhưng cả hai bên có thể có tính liên tục không giống như trong Tập hợp hữu hạn nơi có cả phần tử bắt đầu và kết thúc.
- Nếu một tập hợp có số phần tử không giới hạn thì nó là vô hạn và nếu các phần tử đếm được thì nó là hữu hạn.
Biểu diễn đồ họa của các tập hợp hữu hạn và vô hạn
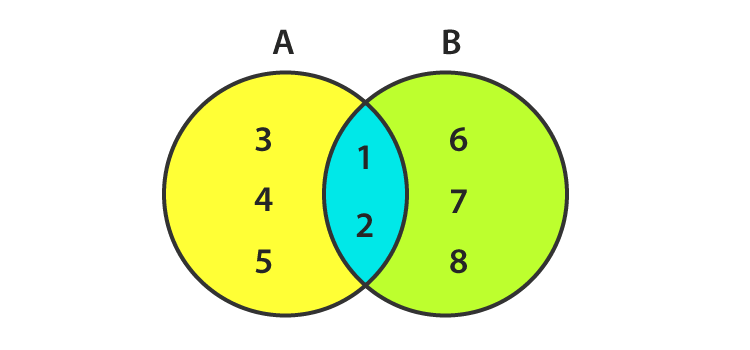
Đây trong hình trên,
A = {1, 2, 3, 4, 5} B = {1, 2, 6, 7, 8} AUB = {1, 2, 3, 4, 5, 6, 7, 8} A∩B = { 1, 2}
Cả A và B đều là tập hợp hữu hạn vì chúng có một số phần tử giới hạn.
n (A) = 5 và n (B) = 5
AUB và A∩B cũng hữu hạn.
Vì vậy, một biểu đồ Venn có thể đại diện cho một tập hữu hạn nhưng rất khó để làm điều tương tự cho một tập vô hạn vì số lượng phần tử không thể đếm được và bị trả lại trong một vòng tròn.
Xem thêm:
- Tính chất và công dụng của Natri Iodide (NaI) chi tiết nhất
- Bảng cửu chương từ 1 đến Bảng 20
- Tính chất và công dụng của Silicon Dioxide (SiO2) chi tiết nhất
- Số tự nhiên là gì? Xem xong 5 phút hiểu luôn.
