Việc nắm vững về các thuật toán máy tính không phải là khủng khiếp với tất cả mọi người. Đa số những người mới bắt đâu sẽ học về đệ quy. Nó đơn giản để học và sử dụng, nhưng điều đó có giải quyết được mục tiêu của bạn. Tất nhiên là không, bởi vì bạn có thể làm được nhiều hơn chứ không chỉ là hồi quy dữ liệu nào đấy. Các thuật toán máy tính (machine learning algorithms), xem chúng như một kho vũ khí với rất nhiều chủng loại rìu, cưa, cuốc, xẻng, súng, lựu đạn..v.v, bạn có nhiều công cụ khác nhau, nhưng cần phải học cách sử dụng chúng vào đúng thời điểm. Như là một phép loại suy, suy nghĩ về việc “đệ quy” như là một thanh kiếm có thể cắt và chia dữ liệu một cách hiệu quả, nhưng nó không có khả năng xử lí với các dữ liệu rất phức tạp. Ngược lại Support Vector Machines (SVM) như là một con dao nhỏ sắc nhọn- nó hoạt động trên các tập dữ liệu nhỏ. nhưng trên đó nó có khả năng xử lí mạnh mẽ hơn trong việc xây dựng các mô hình.
SVM là một thuật toán giám sát, nó có thể sử dụng cho cả việc phân loại hoặc đệ quy. Tuy nhiên nó được sử dụng chủ yếu cho việc phân loại. Trong thuật toán này, chúng ta vẽ đồi thị dữ liệu là các điểm trong n chiều ( ở đây n là số lượng các tính năng bạn có) với giá trị của mỗi tính năng sẽ là một phần liên kết. Sau đó chúng ta thực hiện tìm “đường bay” phân chia các lớp. Đường bay – nó chỉ hiểu đơn giản là 1 đường thằng có thể phân chia các lớp ra thành hai phần riêng biệt. 
Support Vectors hiểu một cách đơn giản là các đối tượng trên đồ thị tọa độ quan sát, Support Vector Machine là một biên giới để chia hai lớp tốt nhất.
Ở trên, chúng ta đã thấy được việc chia hyper-plane. Bấy giờ làm thế nào chúng ta có thể xác định “Làm sao để vẽ-xác định đúng hyper-plane”. Chúng ta sẽ theo các tiêu chí sau:
– Identify the right hyper-plane (Scenario-1):
Ở đây, chúng ta có 3 đường hyper-lane (A,B and C). Bây giờ đường nào là hyper-lane đúng cho nhóm ngôi sao và hình tròn.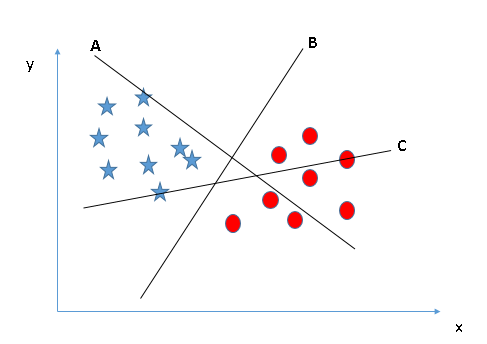 
Bạn cần nhớ quy tắc số một để chọn 1 hyper-lane, chọn một hyper-plane để phân chia hai lớp tốt nhất. Trong ví dụ này chính là đường B
Identify the right hyper-plane (Scenario-2)
Ở đây chúng ta cũng có 3 đường hyper-plane (A,B và C), theo quy tắc số 1, chúng đều thỏa mãn 
Quy tắc thứ hai chính là xác định khoảng cách lớn nhất từ điểu gần nhất của một lớp nào đó đến đường hyper-plane. Khoảng cách này được gọi là “Margin”, Hãy nhìn hình bên dưới, trong đấy bạn có thể nhìn thấy khoảng cách margin lớn nhất đấy là đường C. Ở đây bạn nhớ nếu chọn lầm hyper-lane có margin thấp hơn thì sau này khi dữ liệu tăng lên thì sẽ sinh ra nguy cơ cao về việc xác định nhầm lớp cho dữ liệu
Identify the right hyper-plane (Scenario-3)
Bạn hãy sử dụng các nguyên tắc đã nêu trên để chọn ra hyper-plane cho trường hợp sau 
Có thể có một vài bạn sẽ chọn đường B bởi vì nó có margin cao hơn đường A, nhưng đấy sẽ không đúng bởi vì nguyên tắt đầu tiên sẽ là nguyên tắc số 1., chúng ta cần chọn hyper-plane để phân chia các lớp thành riêng biệt. Vì vậy đường A mới là lựa chọn chính xác.
Can we classify two classes (Scenario-4)?
Tiếp the hãy xem hình bên dưới, mình không thể chia thành hai lớp riêng biệt với 1 đường thẳng, để tạo 1 phần chỉ có các ngôi sao và một vùng chỉ chứa các điểm tròn. 
Ở đây chúng ta sẽ chấp nhận, một ngôi sao ở bên ngoài cuối được em như một ngôi sao phía ngoài hơn, SVM có tính năng cho phép bỏ qua các ngoại lệ và tìm ra hyper-plane có biên giới tối đa . Do đó chúng chúng ta có thể nói, SVM có khả năng mạnh trong việc chấp nhận ngoại lệ. 
Find the hyper-plane to segregate to classes (Scenario-5)
Trong trường hợp dưới đây, chúng ta khong thể tìm ra 1 đường hyper-plane tương đối để chia các lớp, vậy làm thế nào để SVM phân tách dữ liệu thành hai lớp riêng biệt? Cho đến bây giờ chúng ta chỉ nhìn vào các đường tuyến tính hyper-plane 
SVM có thể giải quyết vấn đề này, Khá đơn giản, nó sẽ được giải quyết bằng việc thêm một tính năng, Ở đây chúng ta sẽ thêm tính năng z = x^2+ y^2. Bây giờ dữ liện sẽ được biến đổi theo trục x và z như sau 
Trong sơ đồ trên, các điểm cần xem xét là:
- Tất cả dữ liệu trên trục z sẽ là số dương vì nó là tổng bình phương x và y
- Trên biểu đồ các điểm tròn đỏ xuất hiện gần trục x và y hơn vì thế z sẽ nhỏ hơn => nằm gần trục x hơn trong đồ thị (z,x)
Trong SVM, rất dễ dàng để có một siêu phẳng tuyến tính (linear hyper-plane) để chia thành hai lớp, Nhưng một câu hỏi sẽ nảy sinh đấy là, chúng ta có cần phải thêm một tính năng phân chia này bằng tay hay không. Không, bởi vì SVM có một kỹ thuật được gọi là kernel trick ( kỹ thuật hạt nhân), đây là tính năng có không gian đầu vào có chiều sâu thấm và biến đổi nó thành không gian có chiều cao hơn, tức là nó không phân chia các vấn đề thành các vấn đề riêng biệt, các tính năng này được gọi là kernel. Nói một cách đơn giản nó thực hiện một số biết đổi dữ liệu phức tạp, sau đó tìm ra quá trình tách dữ liệu dựa trên các nhãn hoặc đầu ra mà chúng ra đã xác định trước.
Mình sẽ tìm hiểu và demo về SVM trong mục tiếp theo với python. Thân mọi người đã đọc
