Tính đơn điệu của hàm số là một phần quan trọng trong chương trình toán học. Để củng cố kiến thức tại lớp học và giải các bài tập để các bạn có thể tự ôn luyện tại nhà, bạn đọc hãy tham khảo bài viết dưới đây nhé!
Chúc các bạn hoàn thành tốt môn học.

Lý thuyết về xét tính đơn điệu của hàm số
1. Định nghĩa
D là một khoảng, một đoạn hoặc một nửa khoảng.
Giả sử hàm số y=f(x) xác định trên D
- Hàm số y=f(x) được gọi là đồng biến trên miền D khi và chỉ khi ⇔∀x1,x2∈D và x1<x2 ⇒ f(x1)<f(x2).
- Hàm số y=f(x) được gọi là nghịch biến trên miền D khi và chỉ khi ⇔∀x1,x2∈D và x1<x2 ⇒ f(x1)>f(x2).
2. Định lý
Giả sử y=f(x) có đạo hàm trên khoảng (a;b) thì:
- Nếu f′(x)>0, ∀x∈(a;b) ⇒ hàm số f(x) sẽ đồng biến trên khoảng (a;b).
- Nếu f′(x)<0, ∀x∈(a;b) ⇒ hàm số f(x) sẽ nghịch biến trên khoảng (a;b).
- Nếu f(x) đồng biến trên khoảng (a;b) ⇒f′(x)≥0, ∀x∈(a;b).
- Nếu f(x) nghịch biến trên khoảng (a;b) ⇒f′(x)≤0, ∀x∈(a;b).
Khoảng (a;b) được gọi chung là khoảng đơn điệu của hàm số.
Lưu ý:
Nếu f’(x)=0, ∀x∈(a;b) thì f(x) không đổi tên (a;b).
Nếu thay đổi khoảng (a;b) bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm giả thiết hàm số xác định và liên tục trên đoạn hoặc nửa khoảng đó.
2. Điều kiện cần để hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
- Nếu f đồng biến trên K thì f'(x) ≥ 0 với mọi x ∈ K.
- Nếu f nghịch biến trên K thì f'(x) ≤ 0 với mọi x ∈ K.
3. Điều kiện đủ để hàm số đơn điệu
Cho hàm số f có đạo hàm trên K.
- Nếu f'(x) > 0 với mọi x ∈ K thì f đồng biến trên K.
- Nếu f'(x) < 0 với mọi x ∈ K thì f nghịch biến trên K.
- Nếu f'(x) = 0 với mọi x ∈ K thì f là hàm hằng trên K.
4. Định lý mở rộng
Cho hàm số y=f(x) có đạo hàm trên K.
a) f'(x)0 x K và f'(x)=0 xảy ra tại một số hữu hạn điểm của K thì f(x) đồng biến trên K.
b) f'(x)0 x K và f'(x)=0 xảy ra tại một số hữu hạn điểm của K thì f(x) nghịch biến trên K.
5. Quy tắc xét tính đơn điệu của hàm số
- Tìm tập xác định của hàm số.
- Tính đạo hàm f'(x). Tìm xi(i=1,2,3,….,n) mà tại đó đạo hàm f'(x)=0 hoặc không xác định.
- Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Kết luận.
6. Các dạng của bài tập về tính đơn điệu của hàm số
Dạng 1: Tìm khoảng nghịch biến – đồng biến của hàm số
Phương pháp giải:
Cho hàm số y=f(x)
- f'(x)>0 ở đâu thì hàm số y=f(x) đồng biến ở đó.
- f'(x)<0 ở đâu thì hàm số y=f(x) nghịch biến ở đó.
Quy tắc:
- Tính f'(x), giải phương trình f'(x)=0 và tìm nghiệm.
- Lập bảng xét dấu cho f'(x).
- Nhìn vào bảng xét dấu và đưa ra kết luận.
Dạng 2: Đọc khoảng đơn điệu của hàm số bằng đồ thị cho trước
Phương pháp giải:
Nếu đề bài cho đồ thị y=f(x), ta có thể nhìn vào các khoảng đi lên hoặc đi xuống.
- Khoảng mà tại đó đồ thị đi lên tức là hàm đồng biến.
- Khoảng mà tại đó đồ thị đi xuống tức là hàm nghịch biến.
Nếu đề bài cho đồ thị y=f'(x), ta lập bảng biến thiên của hàm số y=f(x) như sau:
- Tìm nghiệm của f'(x)=0.
- Xét xấu f'(x) (phần trên của 0x mang dấu dương, phần dưới 0x mang dấu âm).
- Lập bảng biến thiên của y=f(x) rồi suy ra kết luận.
Dạng 3: Tìm m để hàm số y=ax+bcx+d đơn điệu trên từng khoảng xác định
Phương pháp giải:
Tính y’=ax+b(cx+d)2
- Hàm số sẽ đồng biến trên từng khoảng xác định của nó y’>0ad-cb>0.
- Hàm số sẽ nghịch biến trên từng khoảng xác định y'<0ad-cb<0.
Dạng 4: Tìm m để hàm số y=ax3+bx2+cx+d đơn điệu trên ℝ
- Hàm số đồng biến trên ℝ thì y’0, xℝ a>0 và y’0 hoặc suy biến a=0, b=0 và c>0.
- Hàm số nghịch biến trên ℝ thì y’0, xℝ a<0 và y’0 hoặc suy biến a=0, b=0 và c<0.
Dạng 5: Tìm tham số m để hàm số lượng giác đơn điệu trên một khoảng cho trước
Dạng 6: Tìm khoảng đơn điệu khi biết đồ thị hàm f'(x)
- Loại 1: Cho đồ thị y=f'(x), tính đơn điệu của hàm y=f(x).
- Loại 2: Cho đồ thị hàm số y=f'(x), tính đơn điệu của hàm số y=f(u).
- Loại 3: Cho đồ thị y=f'(x), tính đơn điệu của hàm hợp y=g(x), trong đó g(x) có liên hệ với f(x).
Dạng 7: Biện luận được tính đơn điệu của hàm đa thức trên khoảng con của ℝ
- Loại 1: Tìm điều kiện của tham số để hàm số y=ax3+bx2+cx+d đơn điệu trên ℝ.
- Loại 2: Tìm điều kiện của tham số để hàm số y=ax3+bx2+cx+d đơn điệu trên khoảng con của ℝ.
- Loại 3: Tìm điều kiện của tham số để hàm số y=ax4+bx2+c đơn điệu trên khoảng con của ℝ.
Bài tập tính đơn điệu của hàm số sgk chọn lọc
1 – Bài 1 trang 9 SGK giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số: a) y=4+3x−x2; b) y=13×3 + 3×2−7x−2;
Hướng dẫn giải:
a) Tập xác định: D=R.
Có y′=3−2x⇒y′=0 ⇔3−2x=0 ⇔x= .
Bảng biến thiên:
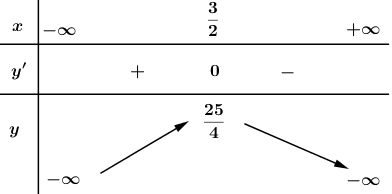
Vậy hàm số sẽ đồng biến trên khoảng (−∞;) và nghịch biến ở trên khoảng (;+∞).
b
y= x3+3×2−7x−2
Tập xác định: D=R.
Có y′=x2+6x−7 ⇒y′=0 ⇔ x2+6x−7=0⇒y′=0 ⇔ 
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng (−∞;−7) và (1;+∞).
Hàm số nghịch biến trên (−7; 1).
c) y=x4−2×2+3
Tập xác định: D=R.
Có y′=4×3−4x ⇒y′=0 ⇔ 4×3−4x=0
⇔4x(x2−1)=0
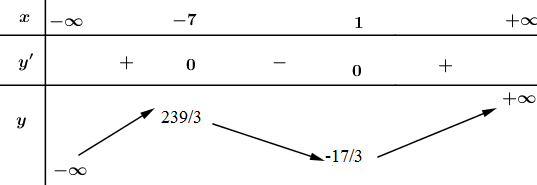
Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng (−1; 0) và (1;+∞).
Hàm số nghịch biến trên các khoảng (−∞;−1) và (0; 1).
d) y= −x3+x2−5
Tập xác định: D=R.
Có y′=−3×2+2x ⇒y′=0⇔−3×2+2x=0 ⬄
Bảng biến thiên:
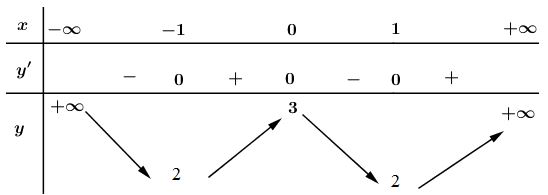
Vậy hàm số đồng biến trên khoảng (0; ).
Hàm số nghịch biến trên các khoảng (−∞;0) và (;+∞).
2 – Bài 2 trang 10 SGK giải tích 12
Tìm các khoảng đơn điệu của các hàm số: a) y=
b) y=
c) y=
d) y=
Hướng dẫn giải:
a) Tập xác định : D = R{ 1 }
. 
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R{ 1 }.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
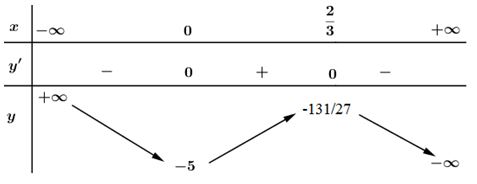
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R{ -3 ; 3 }. 
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).
3 – Bài 3 trang 10 sgk giải tích 12.
Hãy chứng minh rằng hàm số sẽ đồng biến trên khoảng (-1 ; 1) và nghịch biến trên các khoảng (-∞ ; -1) và (1 ; +∞).
Hướng dẫn giải:
Tập xác định : D = R.
⇒ y’ = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).
4 – Bài 4 trang 10 sgk giải tích 12.
Hãy chứng minh rằng hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).
Hướng dẫn giải:
Tập xác định : D = [0 ; 2]; , ∀x ∈ (0 ; 2); y’ = 0 ⇔ x = 1.
Bảng biến thiên :
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).
5 – Bài 5 trang 10 sgk giải tích 12.
Hãy chứng minh được các bất đẳng thức sau:
a) tanx > x (0 < x < ;
b) tanx > x +x3/3 (0 < x <).
Hướng dẫn giải:
a) Ta xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = – 1 ≥ 0, x ∈ [0 ; ); y’ = 0 ⇔ x = 0. Vậy hàm số đó luôn đồng biến trên [0 ;).
Từ đó ∀x ∈ (0 😉 thì f(x) > f(0) ⇔ tanx – x > tan 0 – 0 = 0 hay tanx > x.
b) Ta xét hàm số y = g(x) = tanx – x – . với x ∈ [0 ; ).
Ta có : y’ = – 1 – x2 = 1 + tan2x – 1 – x2 = tan2x – x2
= (tanx – x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx – x >0 (theo câu a).
Do đó y’ ≥ 0, ∀x ∈ [0 ; ). Dễ thấy y’ = 0 ⇔ x = 0. Suy ra hàm số đó luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ; ) thì g(x) > g(0)
⇔ tanx – x – >( tan 0 – 0 – 0) = 0
Suy ra tanx > x + .
Trên đây là tổng hợp lý thuyết và cách giải một số dạng bài tập về Tính đơn điệu của hàm số – một chương chủ đạo. Các bạn học sinh cần nắm vững kiến thức của chương này.
Nhằm giúp các bạn học sinh nắm vững kiến thức trên lớp và có thể tự ôn tập tại nhà, chúng tôi cung cấp lời giải chi tiết nhất và bám sát vào chương trình giảng dạy. Chúc các bạn học tập tốt và đạt kết quả cao trong môn học này.
